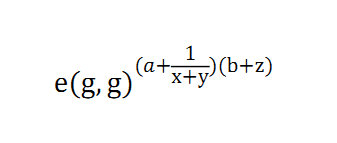本次澳洲代写是现代密码学的一个assignment

Note: The questions will be added after each week (from week 6 to week 11)

Task A: (Week 6, 4 marks)

Let f(x) be a One-Way Homomorphic Function where f(kp+1)=f(1) for any integer k and a big prime p. Given the value f(1) and the ElGamal ciphertext CT=(f(r), f(r*b)⊕M) where pk=f(b)
and sk=b. Here, r is a random number chosen by the encryptor and f(r*b) is a bit string.

Q1: Show how to quickly compute f(111) step by step. (2 marks)

Q2a: Show how to break the ElGamal ciphertext in details. An inefficient solution is
acceptable (2 marks). This question is for CSCI471 students only.

Q2b: Suppose that the output f(x) for all x has the problem that the first bit (MSB) is equal
to 1 with probability 99.9999%. Show how to break the ElGamal ciphertext in the IND-CPA
security model. (2 marks). This question is for CSCI971 students only.

Task B: (Week 7, 4 marks)

In the RSA signature scheme, suppose that the adversary is given the signatures on message
2 and 3. What messages can the adversary forge their signatures? (You are asked to show 5
different messages and explain how to forge one of signatures.) (2 marks).

In the Schnorr signature scheme, suppose that the random number r chosen by the signer
must be integers 1 or 2. That is, r cannot be other random numbers. Prove that the adversary
can totally break via chosen-message attacks. (2 marks)

Task C: (Week 8, 4 marks)

Given the bilinear pairing group (G,G_T,e, g,p) , group elements (g^a, g^b) and integers
(x,y,z), show how to efficiently compute the following elements step by step. (Important: a
and b are unknown)