这是一个美国的离散微分几何代写
Exercise 3.1 — 15 pts. A spherical polygon is a region on the sphere bordered by great circles. In this exercise you will show that the sum ˝i θi of the exterior angles θi of a spherical polygon is 2π − A, where A is the area enclosed by the spherical polygon.
(a) 5 pts. Show that the area A of a spherical triangle on the unit sphere with interior angles α1;α2;α3 is
A = α1 + α2 + α3 − π: (1)
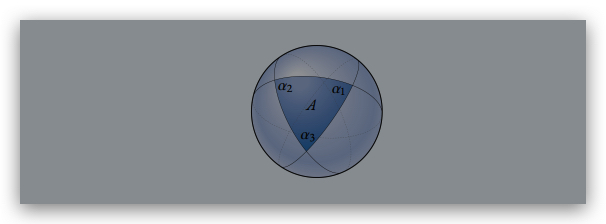
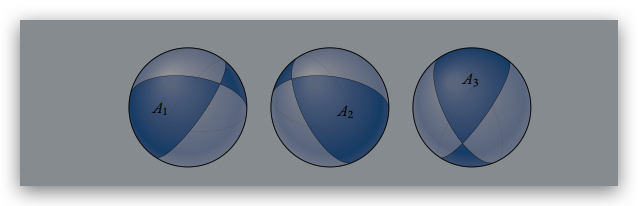
Hint Consider the areas A1;A2;A3 of the three spherical lunes.
(b) 5 pts. Show that the area of a spherical n-gon with interior angles β1; : : : ; βn is


Hint Partition the polygon into triangles.
(c) 5 pts. Conclude that the area of a spherical n-gon with exterior angles θ1; : : : ; θn is
