本次代写是一微观经济的assignment
Consider the following sample of home prices (in thousands of dollars) and number of bedrooms:
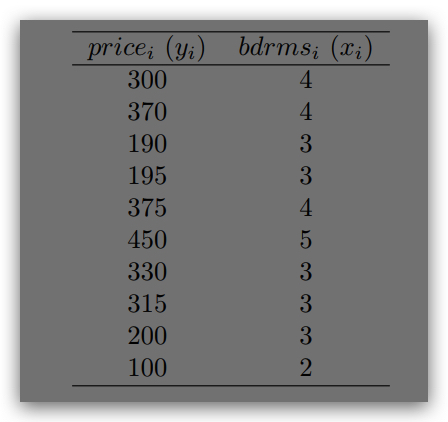
You believe there is a causal relationship between the number of bedrooms and the value of the house,
so you seek to estimate the following equation:
pricei = β0 + β1bdrmsi + ui
1. Using your sample of 10 homes, what are your least squares estimates of β0 and β1? Recall that
β^1 = Pn iP(xn ii(−xxi−)(xy)i2−y) and β^0 = y − β^1x. You must show your workings/tabulations. Please use Excel
for tabulations (or Google Sheets).
2. Write your sample regression function (i.e. simply replace β0 and β1 in the equation above with your
estimates of them, β^0 and β^1 and drop ui). What is your interpretation of β^1?
3. Plot your sample regression function. Place your 10 data points on the same chart to see how the line
\fits” the data. Plot this as carefully as possible if you do it by hand.
4. Calculate the predicted (or \fitted”) values of pricei, price [i, for each observation. Fill in the third
column of the table below with your calculations. Recall that the predicted value for observation i is
given by ^ yi = β^0 + β^1xi.
5. Calculate the residuals for each observation. Fill in the fourth column of the table below with your
calculations. Recall that the residual for observation i is ^ ui = yi − y^i. What is the sum of these
residuals? Place it in the space underneath the column.
6. Fill in the fifth column below, which is simply the square of each residual, ^ u2 i . Sum up these values
to obtain what is known as the sum of squared residuals, SSR. Place it in the space underneath the
column.
