这是美国作业案例,主要为一个数学凸优化作业的数学代写
Part I: True or False: Explain your answer with one sentence (27 pts)
I.1 (convex set): Set {(x2, y2)|x + y ≥ 4, x, y ∈ R+} is convex.
T/F:
I.2 (dual cone): Given cone K = {x|Ax ≥ 0, x ∈ Rn}, where A ∈ Rm×n its dual
cone is K∗ = {y|AT y ≥ 0, y ∈ Rm}.
T/F:
I.3 (Convex Function): Given a function f(x) = log(ea1x1 + ea2x2 + ea3x3) with
domain D = {x|x ∈ R3}, we can show that f(x) is a convex function for every
arbitrary vector a ∈ R3.
T/F:
I.4 (Conjugate Function): Given function f(x) = x2 1−4x1x2+x2 2, where x ∈ R2,
then the conjugate of the conjugate function, f ∗∗(x), is equal to itself, i.e.,
f ∗∗(x) = f(x).
T/F:
I.5 (Convex Function): Function g(x) = minyf(x, y) is convex function, if
f(x, y) is a convex function with respect to variable x.
T/F:
I.6 (Convex Function): Given a differentiable but nonconvex function f(x),
where x ∈ Rn, and a fixed point ¯ x ∈ Rn, the hyperplane
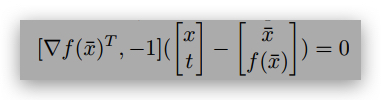
is a supporting hyperplane of epigraph, epi f = {!xt” |f(x) ≤ t}.
T/F:
I.7 (Problem Formulation): For every convex optimization problem defined as
eq. (4.1) in textbook, where all functions are convex, there is always an optimal
solution.
T/F:
I.8 (Problem Formulation/Duality): Given a convex programming problem:
minimize f0(x), subject to Ax ≤ b, x ∈ Rn, A ∈ Rm×n, b ∈ Rm,
where f0(x) is a differentiable convex function, we can claim that
∇f0(¯ x) ∈ {−AT θ|θ ∈ R+m}
is a necessary condition for ¯ x to be an optimal solution.
T/F:
I.9 (Duality): Given a function f(x, y), the inequality
minxmaxy − f(x, y) ≥ maxyminx − f(x, y)
is always true.
T/F:
Part II: Problem Solving: Show your process
Problem 1. Dual Cone: Find the dual cone of the following cones. (20 pts)
1.1. K = {!xt” |||x||p ≤ t}, where p ≥ 1.
1.2. K = {!xt” |||x||p ≤ t}, where 0 < p < 1.
Problem 2. Conjugate Function: Find the conjugate function of the following
functions. (20 pts)
2.1. f(x) = x1x2, where x ∈ R+2 .
2.2. f(x) = #|| a1x−||pp p1,||x||p, || ||x x|| ||p p ≤ > a, a,
where variable x ∈ Rn, constants a ∈ R++, and p ≥ 1.
Problem 3. Graph Embedding. (33 pts)
Following Homework 4 Assignment II.2 Graph Embedding problem context
and notations, our problem statement is the following.
minx1,y1∈Rn−kx%
1 L&x1 + y1%L&y1 + b%x1 + d%y1.
subject to 1T x1 = 0, 1T y1 = 0,
where 1 is a vector of 1s, i.e. the sum of elements in x1 is zero, and the sum
of elements in y1 is zero. Note that in contrast to Homework 4, we don’t have
quadratic constraints. Instead, we have linear equations.