这是一篇英国的多元数据分析数学代写
Question 1. (20 points)
Consider a ℝ2 Gaussian random vectorx = (X,X,)T and a matrix A∈ℝ3×2; assume that
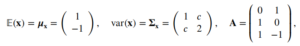
with c ∈ ℝ. Introduce z = (Z1 , Z2 , Z3)T = Ax.
(a) Give the condition on c for the matrix ∑x to be a covariance matrix. [2]
(b) For which value of c do we have X1 ⟂⟂ X2 ? [2]
Assume that c is such that the matrix ∑x is a covariance matrix.
(c) Compute E(z) and var(z), and give the distribution of z. [7]
Hint: Compute each entry of the vector E(z) and of the matrix var(z); note that var(z) should depend on c.
Consider the vector v = (1,−1, 1)푇 ; note that ATv = 0.
(d) Use the vector v to defifine a principal component of z, and give the variance of this principal component. [3]
(e) What is the fraction of variance explained by the fifirst two principal components of the random vector z? For which values of c does the fifirst principal component of the random vector z explain 100% of its variance? [4]
Hint: You may consider det(∑x).
(f) Give an expression for Z3 in terms of Z1 and Z2 . [2]
Question 2. (11 points)
Consider a centered Gaussian process (Zx)x∈ℝ with covariance kernel K(x, x′ ) = e−|x−x′|, for x and x′ ∈ ℝ.
Assume that the realisation Z0 = z0 was observed, with z0 ∈ ℝ (i.e. observation at x = 0). Consider x and x′ ∈ ℝ.
(a) Give the distribution of the random variable Zx|Z0=z0 . Draw a scheme illustrating the appearance of the map x ↦ E (Zx|Z0 = z0) , withx ∈ℝ. [7]
(b) Compute c-cov (Zx , Zx′ | |Z0 = z0) ; what can be concluded forx < 0 and x′ > 0? [4]
Question 3. (21 points)
Consider two independent random samples x1, ⋯ , xnx i.i.d. x ∼ Nd(Ux, ∑), and y1, ⋯ , yny i.i.d.y ∼ Nd(uy, ∑). Note that these two samples are defifined from Gaussian distributions withsamecovariance matrix, but with potentially difffferent means; the sample related to x is of size nx, and theone related to y is of size ny (and the random vectors xi and yi are independent for alli ∈ {1, ⋯ , nx}and j∈ {1, ⋯ , ny}). Let {̄x, Sx} and {̄y, Sy} be the corresponding sample mean and corrected (i.e.unbiased) sample covariance estimators. Consider the pooled variance estimator