这是一篇美国的数值分析数学代写
- Consider the IVP:
y0 = y 0 ≤ t ≤ 1 y(0) = 1. (1)
(a) Use Euler Method to fifind an approximation to y(0.5) for this IVP with ∆t = 0.5.
(b) Reduce ∆t by half (∆t = 0.25) and compute the corresponding approximation to y(0.5).
(c) Use Richardson extrapolation and (a)-(b) to produce a more accurate approximation to y(0.5).
- Consider the initial value problem:
y 00 − 2y0 + y = tet − 1 0 ≤ t ≤ 1, (2)
y(0) = y0 (0) = 0. (3)
(a) Transform this problem into an IVP for a fifirst order system of ODEs.
(b) Take the time step size ∆t = 0.1. Do one step of midpoint method
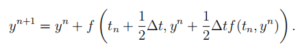 (4)
(4)
(c) Using (b), compute an approximation of the solution at t = 0.3 with the explicit 2-step Adams method.
- Consider the 2-stage RK method
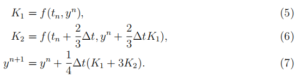
(a) Prove that this method is convergent to the solution of the IVP y0 = f(t, y),0 < t ≤ T, y(0) = α (you may assume f is continuous and Lipschitz in y).
(b) Find the stability function R(z) for this RK method and prove that
R(z) = ez + O(z3). (8)
Infer from (8) the order of the method.
(c) Find the interval of A-stability of this method. This is the intersection of its A-stability region S with the real (x) axis.
- Consider the 2-step method
yn+1 = yn + 1/3∆t(3f n − 2f n−1). (9)
Discuss D-stability, consistency, and convergence for this method.
- Consider the method
yn+1 = yn + ∆t /10[5f n+1 + 4f n − f n−1]. (10)
(a) What type of method is it?
(b) Is it convergent?
- Consider the multi-step method
yn+1 = 5yn−1 − 4yn + ∆t[4f n + 2f n−1]. (11)
Discuss consistency, D-stability, and convergence.
- Find the region of A-stability (linear stability) of (a) the forward Euler method and (b) the backward Euler method.
- Write the RK methods corresponding to the following Butcher tableaux in Tables 1-2.