本次澳洲作业代写案例是一个微积分相关的quiz数学代写
Question 1
Let S = fv1; v2; v3; v4; v5g be a set of five vectors in R3. Let W = spanfSg. When these vectors
are placed as columns into a matrix A as A = (v1 j v2 j v3 j v4 j v5) and A is row-reduced to
echelon form U, we have

1. State the dimension of W.
2. State a basis B for W, using vectors vi with i as small as possible.
3. Express v5 as a linear combination of the basis vectors in B.
W = spanfSg = Ax, x 2 R5. Since A can be row-reduced to echelon form U and U has 3
leading columns, then W has dimension 3.
Since dim(spanfSg) = 3 and the first three columns of U are leading columns, we can take
the first three vectors of S to form a basis of W: B ={v1, v2, v3}.
If we take x = (x1; x2; x3; x4; x5)T then Ax = 0 can be row reduced to Ux = 0:

Let x4 = 0 and x5 = 1. Hence we have x3 = −3, x2 = 8 and x1 = 25, i.e. 25v1+8v2−3v3+v5 =
0. So, v5 =-25*v1-8*v2+3*v3.
Question 7
1. Find the nullity of the matrix

2. Select all statements below which are true.
• (−1; −2; 1; −2; 1)T is in ker A.
• (0; 0; 0; 0)T is in ker A.
• (54; −20; −56; 39)T is in ker A.
• ker A is a subspace of R5.
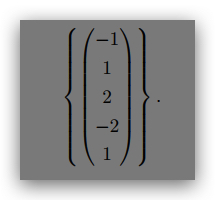
• (−1; 1; 2; −2; 1)T is in ker A.
• (46; 60; −119; 16)T is in ker A.
• ker A is a subspace of R4.
• (0; 0; 0; 0; 0)T is in ker A.
By defining A in Maple as given, we can find a basis for the kernel of A using the command
NullSpace(A). This gives us the basis