这是一篇英国的金融数学作业代写限时测试
- Force of interest
The force of interest is predicted to be the following function r of time t (in years)
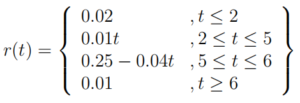
What is the constant annual rate of interest that, with monthly compounding, would give the same increase in value from t = 1 to t = 7?
- 2.75.1 X
- 0.0275.001 X
We are looking for the constant r satisfying
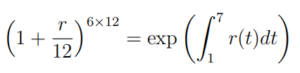
Computation shows R 17 r(t)dt = 0.165. Hence r = 12(exp(0.165)1/72 − 1) ≈ 0.027
- Annuities
You are comparing mortgage offffers from difffferent building societies and are interested in the following two options for a loan of 120, 000:
(1) interest rate of 1.68% for the fifirst 5 years and then 3.54% for the remaining term. No additional fees are charged.
(2) fifixed interest rate of 2.34% throughout the term but an additional fee of 1, 000 is added to the loan.
Assuming that interest is converted at the end of every month, which of the following are true?
(a) Assuming a monthly repayment of 760, the remaining debt after 5 years for offffer (1) would be approximately 82, 972.51. (50%)
(b) The monthly repayment to clear the debt after 20 years for offffer
(2) is A = 749.43 (−50%)
(c) Assuming offffer (2) has a term of 20 years, the APR of (2) is 2.43% (50%)
(d) Assuming a monthly repayment of 760, it would take at least 18 years to clear the entire debt for offffer (1). (−50%)
(a) The remaining debt after k conversion periods is calculated by the formula
P(1 +r/n)k − A (1 +r /12)k − 1/r/n
In this particular situation we calculate 120, 000(1 + 0.0168/12 ) 60 − 760(1+ 0.0168/12) 60−1/0.0168/12≈ 82, 972.51
(b) We calculate
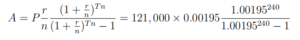
Hence A ≈ 631.79.
(c) Using the result from (b) we can compute the APR a according to the formula
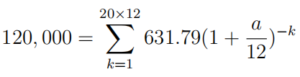
Using the substitution z = (1 +a /12)−1 and the geometric sum on the right hand side we can turn the equation into a polynomial.
The solutions of the polynomial equation can be found found using wolfram alpha or similar (I have shown students how to do this in class and there were plenty of similar exercises on the tutorial sheets).
(d) According to (a) we have a debt of 82, 972.51 after 5 years. We are looking to determine the minimal T such that P(1 +r /12) 12T − A /(1+r/n )12T −1/r/n ≤ 0. After some basic algebraic manipulations this is equivalent to
(1 +r /12)12T ≥ A /A − P r/n
In our case we get
1.0029512T ≥ 1.475066250
which leads to T ≥ 10.9964. In particular, the entire debt would be already cleared after 11 + 5 = 16 years.