本次新西兰作业案例分享是一个离散数学代写的限时测试
1. (Graphs.)
(a) Suppose that G is a connected simple planar graph containing V vertices, E edges and
F faces. Suppose further that each of V; E and F are prime numbers.
Prove that exactly one of V; E or F must be equal to 2.
(b) Suppose that G = (V; E) is a graph on n vertices, where each vertex has degree at least
n=2. Prove that G must be connected.
(c) Let G be the set of all planar simple graphs. Given a planar graph G, let #V (G) denote
the number of vertices in G, and similarly let #E(G); #F(G) denote the number of edges
and faces in G. Define the function f : G —— Z as follows:
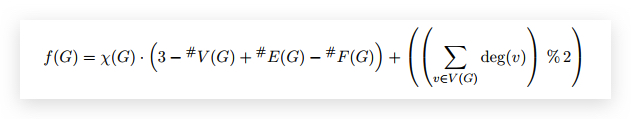
What is the range of f: i.e. what integers are possible outputs of f?
2. (Automata.)
(a) Suppose that we are working over the alphabet Σ = fa; bg. Draw an automata that
recognizes the language of all strings that contain exactly two a’s and two b’s (in any
order.)
(b) Let p be a prime, and let L be the set of all strings over the alphabet fag whose lengths
are multiples of p. Prove or disprove the following claim: \If M is a DFA over the
alphabet fag whose language of accepted strings is L, then the number of states in M is
a multiple of p.”
(c) In class, we proved that you cannot create a DFA over the alphabet fag that accepts
precisely the language L of strings with prime lengths. Prove that you cannot create a
DFA over the language L = fag that accepts precisely the set of strings with nonprime
lengths.
3. (Error-correcting codes.)
(a) Find a ternary length 4 code C with distance 3, containing at least 4 elements.
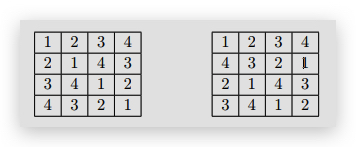
(b) A Latin square (introduced briefly at the end of Lecture 15) is a n × n grid in which
every square contains a number from 1; 2; : : : n, with no repeats in any row or column.
Two 4 × 4 Latin squares are drawn below.
i. Describe how to make a n × n Latin square, for every n.
ii. Given a Latin square, you can make a table of its cells by listing the row, column,
and symbol for each:
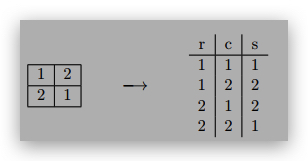
By thinking of the rows of this table as a code, prove that An(3; 2) ≥ n2.