这是一个离散数学代写的限时测试
1. (4 points) Draw representations of the following graphs.
(a) K5
(b) K4;2
2. (4 points) Define the following terms.
(a) degree of a vertex
(b) isomorphism of graphs G1 = (V1; E1) and G2 = (V2; E2)
3. (4 points) Given that a planar graph has 16 regions, one vertex of degree 6 and all other vertices have degree 4, how many vertices are there?
4. (8 points) Is the following graph planar? Why or why not?
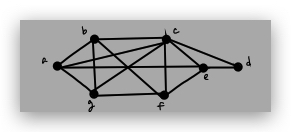
5. True or False. (12 points) Give a brief reason, correction, or counterexample along with your answer.
(a) If two graphs G and H have the same number of edges and vertices, then the graphs are isomorphic.
True False
(b) The number of people at a party who know an odd number of other people must be even.
True False
(c) If a graph is not connected then its complement is connected.
True False
(d) Any planar graph can be (vertex) colored with at most 4 colors but this page is too small to contain the proof.
True False
6. (8 points) Are the following graphs isomorphic to one another? Why or why not?

7. (10 points) Let Km;n;p denote a complete tripartite graph, i.e., a graph whose vertices can be partitioned into three disjoint sets of size m; n; and p, where every vertex in each set has an edge to each and every vertex in the other sets, but not to any in its own set. Determine the values of m; n; and p such that Km;n;p contains an Euler cycle.
How about an Euler trail?
8. (10 points) Choose either of the following homework problems. (Only do one.)
(a) Prove or disprove: If u and v are the only vertices of odd degree in a graph G, then G contains a path from u to v.
(b) Use induction to show that any planar graph can be 6-colored.
9. (10 points) Show that if every vertex of a graph G has degree 3 and G has a Hamilton circuit, then the edges of G can be colored using only 3 colors.