这是一个美国的一个计算机视觉作业代写
Instructions for submission: Please submit a PDF with your solutions on theory questions. The PDF
should explain your work. For coding questions you may use C/C++ and OpenCV or Python with OpenCV
Python for this assignment. Comment your code to make it easier to grade. Include your codes for edge
detection in a folder. Submit a single zip file that contains: 1 – PDF with your answers to question 1; 2
– folder containing edge detection code, images, and readme file that explains how to run your code; 2 –
folder containing your sticks filtering code, images, and readme file that explains how to run your code.
Please submit through Brightspace. You are expected to work on the assignment individually. Do not
leave your submission to the last minute because if you run into technical issues the system will cut you
off. You can submit multiple versions of your assignment, and we will grade the latest one.
1 (30 points) Theory questions
1. (5 points) Are three dimensional rotations expressed as Rx, followed by Ry, and then Rz (rotations
around the x, y and z axis) commutative? That is, does the order in which they are applied matter.
Explain the answer.
2. (8 points) Find the SVD of A, UΣV T , where 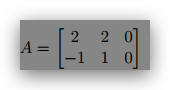
Hint: first find AT A, then find λ by solving det(AT A − λI) = 0. Look at this example to find out
how to calculate the U and V : https://www.d.umn.edu/~mhampton/m4326svd_example.pdf
3. (4 points) Scale a vector [x y]T in the plane can be achieved by x′ = sx and y′ = sy
where s is a scalar.
(a) Write out the matrix form of this transformation.
(b) Write out the transformation matrix for homogeneous coordinates.
(c) If the transformation also includes a translation
x′ = sx + tx and y′ = sy + ty
Write out the transformation matrix for homogeneous coordinates.
(d) What is the equivalent of the above matrix for three-dimensional vectors?
4. (5 points) Find the least square solution x for Ax = b if
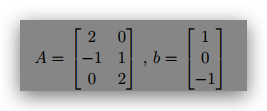
Verify that the error vector b -Ax is orthogonal to the columns of A.
5. Matrix K is a discrete, separable 2D filter kernel of size k × k. Assume k is an odd number. After
applying filter K on an image I, we get a resulting image IK.
(a) (3 points) Given an image point (x, y), find its value in the resulting image, IK(x, y). Express
your answer in terms of I, k, K, x and y. You don’t need to consider the case when (x, y) is near the
image boundary.
(b) (5 points) One property of this separable kernel matrix K is that it can be expressed as the
product of two vectors g ∈ Rk×1 and h ∈ R1×k, which can also be regarded as two 1D filter kernels.
In other words, K = gh. The resulting image we get by first applying g and then applying h to the
image I is Igh. Show that IK = Igh.