本次英国代写是一个非线性规划相关的assignment
Objective: there are two parts to this assignment. In Part A we construct a program for nonlinear
optimization and Part B is the mini research project where you select and investigate an application
of non-linear programming, of your choice. Correct implementation gives 20 marks out of the 40
assigned to the entire assessed coursework for Part A and, for Part B, 20 marks out of 40 are assigned
to the mini research project.
1 Part A
The objective of this part of the project is to implement the conjugate gradient method in either
Matlab or Python. This method has two parameters, as described in the notes, an α parameter and
a β parameter. The α parameter is involved in the update of the position and the β parameter is
involved in the update of the direction vector. For the α update (also indicated as a λ earlier in the
course where the steepest descent method is described), we will find the most appropriate value for
this parameter using a one-dimensional optimization routine. This subpart of the project is described
below. For the β parameter you are free to choose one of the three forms: (a) Hestenes-Stiefel form,
(b) Polak-Riviere form, or (c) Fletcher-Reeves (see p. 82 of notes), or similar, as you wish, though
please indicate your choice as a comment in the code.
The one dimensional line search routine for determining α. This parameter is used in the
update of your position as you move through the multi-dimensional space. I suggest you investigate
and check the performance of your one-dimensional optimizer before using it in the conjugate gradient
program which is described below (perhaps try it out on elementary quadratic programming tasks
before proceding). In the course slides, and not verbally discussed in the lectures, there are various
one-dimensional line search routines that you could use. You will have to investigate this topic,
but you will have come across some of these methods before. For example, you will have used the
Newton Raphson method. In the course slides there is also discussion of the Bisection method.
A recommended routine, which is useful because it operates on a bracketed interval, is called golden
section search in one dimension. You will need to investigate this subject area, but a good pointer
to extensive discussions of these methods is in a book by William Press, Saul Teukolsky, William
Vetterling and Brian Flannery called Numerical Recipes: The Art of Scientific Computing,
Cambridge University Press. This book has gone through a number of additions so I’m not able to
point to specific chapter numbers but these are easily located. The text of the book is free and easily
accessible under numerical.recipes or using a Web search tool for ‘Numerical Recipes’. This book also
mentions conjugate gradient methods and other optimization methods but please note that these are
code blocks for which I will be doing MOSS comparisons against your program.
The materials should be uploaded to the assessment pages of Blackboard for this course and this first
part of the project would have the following components:
(1) The source code for your package for solving a problem using the conjugate gradient method
(e.g. cg.py). If borrowing any code or routines from other sources you must place a reference
(citation) to the original source in the code and any Readme statement to avoid any suspicion
of plagiarised content. There is no mark reduction for the usage of code or commands, e.g.
from numpy, which are reasonably viewed as unrelated to the subject of optimization. For the
usage of code or subroutines from external sources which can be viewed as making it’s easier
to implement a method, there can be a pro rata reduction in marks according to the extent
of borrowed materials from the external source (this assumes a citation is given to the source,
so no plagiarism involved). The course lecturer will use MOSS and other tools to search for
commonality of a program with external sources, and also between students.
(2) It can be difficult drawing a nonlinear objective function from a separate file, as the function to
be optimised. Hence the suggested approach is that the optimization problem to be solved should
be in the form of a function call, or subroutine, to your program. This function or subroutine,
with the objective function, should be clearly commented in the program, preferably at the end
of the program itself.
(3) The conjugate gradient program should be initialised with the following objective function to
minimise:
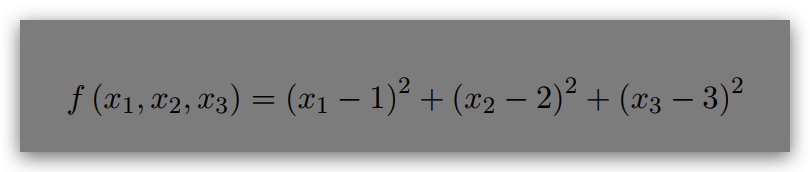
(4) For solving the problem in (3), the program should be initialised at x1 = 0:5; x2 = 0:5; x3 = 0:5.
(5) The initialisation of your variables should be clearly commented at the start of the program,
together with any parameter to be adjusted which states the number of variables.
(6) The problem specification in (3-5) should be clear and easily alterable.
(7) There should be an output file called log.txt which gives internal working steps of the algorithm.
It should give the values of the variables (e.g. x1; x2 and x3) after each step or iteration. However,
without any loss of marks, it is equally fine to use a parameter which will print out the values
of the variables after a fixed number of iterations to avoid an over-long log.txt file.
(8) The algorithm would terminate when there is a small difference between the value of the objective
function between one iteration and the next. This tolerance, which leads to termination of the
program, can be written as, and the value of this parameter should be clearly stated and
alterable at the start of your program.
(9) The program should generate an output file called solution.txt which gives the solution with
an appropriate text indicating which variable is which.
(10) A Readme.txt file which gives extra information as to how to run your program and interpret
the log.txt and solution.txt files