这是一个美国的马尔可夫链作业代写
Problem 1
Recall that a Markov Chain is irreducible if for all w, w′ ∈ Ω, there is a number K = K(w, w′) such that
PK(w, w′) > 0 where P is the transition matrix. Show that there is a universal number N, independent of
the states of the chain, such that PN(w, w′) > 0 for all w, w′ ∈ Ω.
This means that one can go from any step to any other state in N steps.
Hint: there is a really simple solution, if you think of irreducibility from the connectivity perspective.
Problem 2
Irreducibility give us uniqueness of the stationary distribution. A first step to prove this result is the content
of this exercise.
Show that if a Markov Chains is irreducible, then any stationary distribution π satisfy π(w) > 0 for all w ∈ Ω.
Hint: what can you said about the relation between higher powers of P and π? You may want to use the
result from Problem 1.
Problem 3
(Metropolis chain) We saw in class how MC can be used to sample from the stationary distribution. Consider
the following situation: you are given a set Ω and a probability measure π with support equal to Ω. If you
want to sample from this distribution, one idea could be to build a Markov Chain whose state space is Ω
and whose stationary distribution is π. This problem explores one alternative to accomplish this goal.
(a) (Balance equations). Let P(·, ·) be the transition matrix of a Markov Chain with state space Ω, and
let µ(·) be a probability measure such that
µ(x)P(x, y) = µ(y)P(y, x), ∀x, y ∈ Ω.
Show that µ is a stationary distribution by checking that µP = µ.
(b) Consider now a transition symmetric matrix Ψ on Ω (this is, Ψ(x, y) = Ψ(y, x)). You are also given
a set of numbers 0 ≤ p(x, y) ≤ 1. Consider the Markov Chain that moves according to the following
dynamics:
(i) To move from state x, we choose the next state with probability Ψ(x, ·).
(ii) Once we sample the next state (call it y), we flip a biased coin and move to state y with probability
p(x, y) or stay at x with probability 1 − p(x, y) (notice that the success probability of our coins
depend on the states we are looking at).
Write the transition probabilities of this chain. Your answer here should be of the form P(x, y) and
may depend on Ψ and p(·, ·). Make sure to include the case x = y.
(c) Check that, for
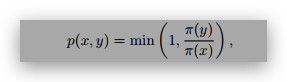
the distribution π is stationary for the chain constructed in part (b).
Hint: combine parts (a) and (b).