本次美国作业案例分享是一个优化相关的数学代写assignment
1 Adagrad: The simple case (40 points)
Show that for function f(x) = f(x1, x2) = ax2 1 + x2 2 for x ∈ R2 and a > 0, if we use Adagrad to optimize f with learning rate η = 1, derive the ratio (as a function of a) of the pre-conditioner:
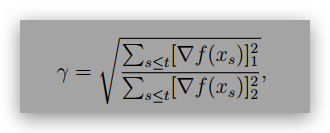
given a fixed initial point x0 = (c, c) where c ̸= 0.
Explain why when a ≫ 1, Adagrad is better than gradient descent
2 Convex optimization but the minimizer is at infinity
Li Hua claims that he has spotted a huge bug in the convergence proof of gradient descent convex functions in the lecture. He claims that the proof can not be applied to logistic regression, where the optimizer is at infinity. Hence gradient descent might take forever to converge.
Now, you want to show him some math:
1. (5 points) For logistic function h(x) = log(1 + ex) as a function h : R → R, show that the minimizer of h is indeed at infinity.
Solution
2. (5 points) However, show that for every ϵ > 0, there is an x such that |x| = O(log(1/ϵ)) with h(x) ≤ ϵ.
Solution
3. (30 points) Now, for general function f : Rd → R, suppose f is L-smooth convex function, and for an ϵ > 0, there is an x with ∥x∥2 ≤ R such that f(x) ≤ ϵ.
Now, show that starting from x0 = 0, gradient descent update with η ≤ L1 :
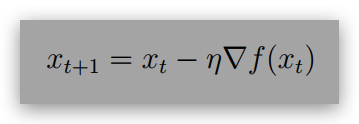
converges to f(xT ) ≤ 2ϵ in T ≤ poly(R, L, 1/η, 1/ϵ) many iterations. (Hint: Apply Mirror Descent Lemma on x)
3 Random Query for Convex Optimization (20 points)
This problem studies the efficiency of the following optimization algorithm for a d-dimensional convex function f:
1. Fix a probability distribution D, which does not depend on f. You don’t know f, but let’s say you somehow know that the optimum x∗ has nonzero probability density over D.
2. Sample x1, x2, …xN ∼ D
3. Return xm = argminx1,…xN f(x)
Let D be the uniform distribution over the cube Q = {x | −1 ≤ xi ≤ 1} = {x | ∥x∥∞ ≤ 1}.
Show that for every fixed x0 ∈ Rd, if we sample N = dO(1) points x1, x2, · · · , xN uniformly from Q, then with probability lower bounded by 1−e−Ω(d), the following holds for all i ∈ [N]: