这是一个来自美国的关于算法设计的作业代写，具体详情可扫码咨询客服

Instructions: As in previous homeworks.

Note: In any dynamic programming solution, you should follow the steps below (if we explicitly
state that pseudocode is not required, then step 4 may be skipped):

1. first give a clear, precise definition of the subproblems (i.e., what the recursive function is
intended to compute);

2. then derive a recursive formula to solve the subproblems (including base cases), with justifi
cation or proof of correctness if the formula is not obvious;

3. specify a valid evaluation order;

4. give pseudocode to evaluate your recursive formula bottom-up (with loops instead of recur
sion); and

5. analyze the running time.

Do not jump to pseudocode immediately. Never skip step 1!

Problem 6.1: For a sequence hb1; : : : ; bmi, an alternation is an index i 2 f2; : : : ; m − 1g such that
(bi−1 < bi and bi > bi+1) or (bi−1 > bi and bi < bi+1).

(a) (80 pts) Given a sequence ha1; : : : ; ani and an integer k ≤ n − 1, we want to compute a
longest subsequence that has at most k alternations.

(For example, for the input sequence h3; 1; 6; 8; 2; 10; 9; 4; 5; 12; 7; 11i and k = 2, an opti
mal subsequence is h1; 6; 8; 10; 9; 4; 5; 7; 11i, which has 2 alternations.)

Describe an O(kn2)-time dynamic programming algorithm to solve this problem.1 In
this part, your algorithm only needs to output the optimal value (i.e., the length of the
longest subsequence).

(b) (20 pts) Give pseudocode to also output an optimal subsequence.

Problem 6.2: We have an n × 4 grid, with n rows and 4 columns. We are given an n × 4 matrix
F, where F[i; j] = 1 indicates that the grid cell at the i-th row and j-th column is forbidden,
and F[i; j] = 0 indicates that the cell is \allowed”. The goal is to cover the maximum number
of grid cells using shapes of the following three types (we are not allowed to rotate these
shapes):

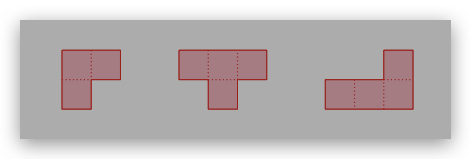
The constraints are: (i) no forbidden cells are covered, and (ii) each cell is covered at most
once (i.e., the shapes can’t overlap).