这是一篇澳洲的MATLAB优化与运筹方法的数学作业Matlab代写,以下是作业具体内容:
Assignment 2.1. (globalised Newton method, 5 marks)
In this task you will implement the globalised Newton method and compare its performance with that of Newton’s met hod.
a) Complete the Matlab file myGlobalisedNewton .m by implement ing the.globalised Newton scheme as stated in Algorithm 4.1, taking the following instruct ions into account:
一Stop the iteration if either |∇f(x)|≤tol or k≥maxstep.
一Consider the linear equation solvable if and only if the condition number of the Hessian (Mat lab command cond) is smaller than or equal to 1010. If it is larger than 1010, do not solve the system.
一Make sure you do not invert the Hessian in the Newton step. Use the backslash operator for the linear solve.
一Please work the Armijo rule into this algorithm and do not call any external code. If you have problems with the Armijo rule, you are now explicitly allowed to ask for help from your peers, your tutors or your lecturer with this part of the task. (The Armijo rule has already been examined in Assignment 1.) Please do not post any implementat ions online where they could be available to third parties.
b) Please run the Matlab script wrapper .2. _1 .m that visualises the performance of your code on the Rosenbrock function
f :R2→R, f(x,y)=(1-x)2 + 100(y-x2)2
and the scalar function
f(x)=x4- 4×2+ 8x,
and answer the follow ing questions:
i) The globalised Newton met hod seems to converge to the minimum z*= (1,1)T of the Rosenbrock function. Based on your know ledge,argue why this does or does not have to be the case.
ii) Based on the graphical output, the wrapper code and the pseudocode provided in Algorithm 4.1, please explain how the met hod chooses its steps in this particular example.
ii) Please explain why exactly the globalised Newton method converges to the minimum of the scalar function above by inspecting the individual steps and decisions that the globalised Newton method makes. Recall that Newton’s method failed to converge in this particular example in Assignment 1.
Assignment 2.2. (inverse BFGS method, 5 marks)
In this task you will implement the inverse BFGS method as stated below and examine its behaviour. The purpose of restating this part icular version of the algorithm is to rule out potent ial ambiguities in the interpretation of the pseudocode in Algorithm 4.8.
Algorithm (inverse BFGS method).
(S0) Choose:
ro∈Rnanda
symmetric positive definite matrix W,∈Rnxn.
(The user tries to supply an approximation Wo of V2f(xo)-1. You sim-
ply use the Wo that the user supplies.) Initialise k←0. Set tolerance
tol > 0 and choose maxstep ∈N.
(S1) If maxstep≤0 or |∇f(xo)|I≤tol, return (xo, Wo, 0).
(S2) Set de←-Wk∇f(xk), set xk+1←Tk +dk and compute the vector yk←∇f(xk+1)- ∇f(xk).
(S3) If k+1≥maxstep or |∇f(xk+1)|≤tol, return (xk+1,Wk,k+ 1).
(S4) If yTdk < 0, terminate with error message ‘BFGS update may not be positive definite’. (Matlab has a command error.)
(S5) Compute the update
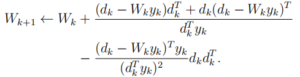
(S6) Set k←k+1 and go to (S2).
Let us examine how the inverse BFGS method works in detail, and how it reacts to initial guesses of the inverse Hessian of diferent quality.
a) Please complete the Mat lab file my InverseBFGS .m by implementing the inverse BFGS method as stated above.
b) Please run the Matlab script wrapper_2_ .2 .m that visualises the behaviour of your code when applied to the scalar function
f(x)=x*+x2- 3x
and the Rosenbrock function, and comment on the behaviour of the quadratic model with approximate Hessian as k: increases.