本次代写是一个Opencv的assignment
1 (30 points) Theory questions
1. (5 points) Are three dimensional rotations expressed as Rx, followed by Ry, and then Rz (rotations
around the x, y and z axis) commutative? That is, does the order in which they are applied matter.
Explain the answer.
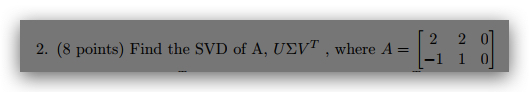
Hint: first find AT A, then find λ by solving det(AT A − λI) = 0. Look at this example to find out
how to calculate the U and V : https://www.d.umn.edu/~mhampton/m4326svd_example.pdf
3. (4 points) Scale a vector [x y]T in the plane can be achieved by x′ = sx and y′ = sy
where s is a scalar.
(a) Write out the matrix form of this transformation.
(b) Write out the transformation matrix for homogeneous coordinates.
(c) If the transformation also includes a translation
x′ = sx + tx and y′ = sy + ty
Write out the transformation matrix for homogeneous coordinates.
(d) What is the equivalent of the above matrix for three-dimensional vectors?
4. (5 points) Find the least square solution x for Ax = b if
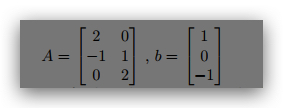
Verify that the error vector b -Ax is orthogonal to the columns of A.
5. Matrix K is a discrete, separable 2D filter kernel of size k × k. Assume k is an odd number. After
applying filter K on an image I, we get a resulting image IK.
(a) (3 points) Given an image point (x, y), find its value in the resulting image, IK(x, y). Express
your answer in terms of I, k, K, x and y. You don’t need to consider the case when (x, y) is near the
image boundary.