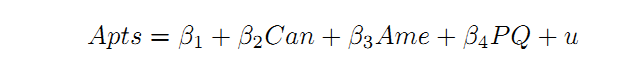本次加拿大代写是一个R数据分析的assignment
In this second assignment, you need to use the data file Players.rda. The dataset includes the individual statistics of NHL players from 1999 to 2012. The variables are
year: The statistics year. For example, year = 1999 means the 1999-2000 season. Note that the season 2004-2005 was cancelled, so no data is available for year = 2004.
- Player: The player’s name
- country: The player’s country of origin.
- state: For Canadian or American players, it is the player’s state or province of origin.
- weight: Player’s weight in pounds.
- height: Player’s height in inches.
- age: PLayer’s age in years.
- gp: The number of games played.
- g: The number of goals.
- a: The number of assists.
- pts: The number of points (a+g).
- Pos: The player’s position: C = Center, L = Left wing, R = Right wing.
To avoid having outliers caused by players who did not play many games, restrict your sample to players who played more than 40 games using the following code.
load(“Players.rda”)
dat <- subset(dat, gp>40)
Also, we want the dependent variable to be a measure of productivity defined as the average number of points (APts) per 50 games. You can create this variable as follows (it is also added to the dataset)
dat$Apts <- dat$pts/dat$gp*50
For this document, I want you to hide all your codes (e.g. using echo=FALSE). I only want to see your comments, interpretations and results (using Latex tables, my printEqu function to print regression results or any other packages)
Question 1
What kind of dataset do we have here? Do we have iid observations? What should we expect in terms of the properties of OLS? Can we consider this dataset to be a sample coming from a larger population?
Question 2
Create a dummy variable for Canadian players (Can) and one for American players (Ame). Then, estimate the following model:
a. Interpret the meaning and significance of each coefficient.
b. Analyze the statistical properties of the residuals. Do you see any reason to believe that the classical assumptions are violated? Do you detect any influential observation?
c. Test the hypothesis H0 : β2 = β3. Make sure you use a heteroskedasticity robust test if needed. What are we testing here?
d. What happens if you add a dummy variable PQ equal to 1 if the player was born in Quebec and 0 otherwise? Estimate the model and interpret all coefficients:
EasyDue™ 支持PayPal, AliPay, WechatPay, Taobao等各种付款方式!
E-mail: easydue@outlook.com 微信:easydue
EasyDue™是一个服务全球中国留学生的专业代写公司
专注提供稳定可靠的北美、澳洲、英国代写服务
专注提供CS、统计、金融、经济、数学等覆盖100+专业的作业代写服务