这是一个澳洲的R统计线性模型的的作业代写
Instructions to Students
- This assignment is worth 6% of your total mark.
- You may choose to either typeset your assignment in LATEX, or handwrite and scan it to
produce an electronic version. - You may use R for this assignment, but for matrix calculations only (you may not use the
lm function). If you do, include your R commands and output. - Write your answers on A4 paper. Page 1 should only have your student number, the
subject code and the subject name. Write on one side of each sheet only. Each question
should be on a new page. The question number must be written at the top of each page.
Scanning and Submitting - Put the pages in question order and all the same way up. Use a scanning app to scan all
pages to PDF. Scan directly from above. Crop pages to A4. - Submit your scanned assignment as a single PDF file and carefully review the submission
in Gradescope. Scan again and resubmit if necessary.
Question 1 (4 marks)
Let A be an idempotent n × n matrix. Find all scalars k such that the matrix I − kA is
idempotent.
Question 2 (5 marks)
Prove (without using Theorem 2.5) that if A and B are symmetric matrices, A+B is idempotent
and AB = BA = 0, then both A and B are idempotent. (Hint: Use Theorem 2.4. Then derive
two relations between the diagonalisations of A and B.)
Question 3 (10 marks)
Let y be a 3-dimensional multivariate normal random vector with mean and variance
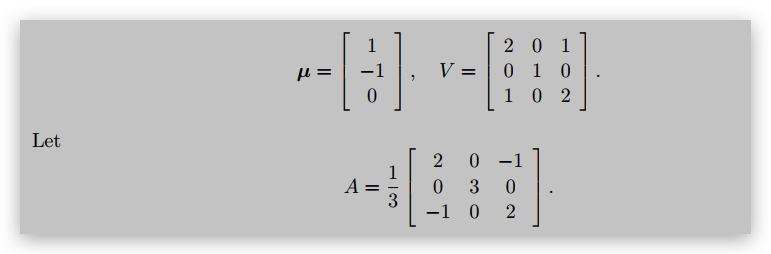
(a) Describe the distribution of Ay.
(b) Find E[yT Ay].
(c) Describe the distribution of yT Ay.
(d) Find all matrices B such that yT By is independent of yT Ay.
Question 4 (4 marks)
Let AB = Im, where A is an m × n matrix and B is an n × m matrix. If y ∼ MV N(µ, In) and
BA is symmetric, find the distribution of yT BAy.
Question 5 (8 marks)
A manager wants to know if (and how) the sales figures of each store is dependent on the
advertising cost and the size of the store. A linear model is assumed, and the following data is
obtained from six stores:
Sales ($k) Advertising cost ($k) Size (m2)
227 2 200
354 4 250
373 5 200
512 6 400
537 8 150
328 4 220
(a) Write down the linear model as a matrix equation, writing out the matrices in full.
(b) Calculate the least squares estimate of the parameters.
(c) Calculate the residual sum of squares SSRes and sample variance s2.
(d) Predict (using a point estimate) the average sales figure of a store with $3k advertising
cost and 350m2 size.
Question 6 (5 marks)
Let A be a symmetric and idempotent matrix with entries aij. Prove that 0 ≤ aii ≤ 1. Use this
to derive limits on the leverage of a point in the full rank model.