这是一个加拿大的实践理论统计代写
1. The Hidalgo stamp data is a (semi-)famous dataset containing thicknesses of 486 postage
stamps from the 1872 Mexican \Hidalgo” issue. It is believed that these stamps were printed
on different types of papers so that the data can be modeled as a \mixture” of several
distributions with the density having between 5 and 7 modes. These data (which have been
“jittered” by adding noise) are available on Quercus in a file stamp.txt.
(a) Use the density function in R to estimate the density. Choose a variety of bandwidths
(the parameter bw) and describe how the estimates change as the bandwidth changes. How
small does the bandwidth need to be for the density estimate to have 5 modes? 7 modes?
(b) One automated approach to selecting the bandwidth parameter h is leave-one-out
cross-validation. This is a fairly general procedure that is useful for selecting tuning
parameters in a variety of statistical problems.
If f and g are density functions, then we can define the Kullback-Leibler divergence
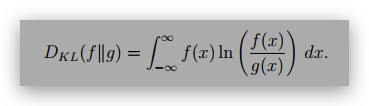
For a given density f, DKL(f||g) is minimized over densities g when g = f (and DKL(f||f) =
0). In the context of bandwith selection, define fbh(x) to be a density estimator with band
width h and f(x) to be the true (but unknown) density that produces the data. Ideally, we
would like to minimize DKL(f||fh) with respect to h but since f is unknown, the best we
can do is to minimize an estimate of DKL(f||fh). Noting that

this suggests that we should try to maximize an estimate of Ef[ln(fh(X))], which can be
estimated for a given h by the following (leave-one-out) substitution principle estimator:
